Option Greeks measure sensitivity of option prices to underlying factors like delta, gamma, theta, and vega, providing crucial insights for risk management and strategic trading. Option skew reflects the market's implied volatility differences across strike prices and expiration dates, indicating sentiment and potential price direction biases. Explore the nuances of Option Greeks and Option Skew to enhance your options trading strategies and risk assessment techniques.
Main Difference
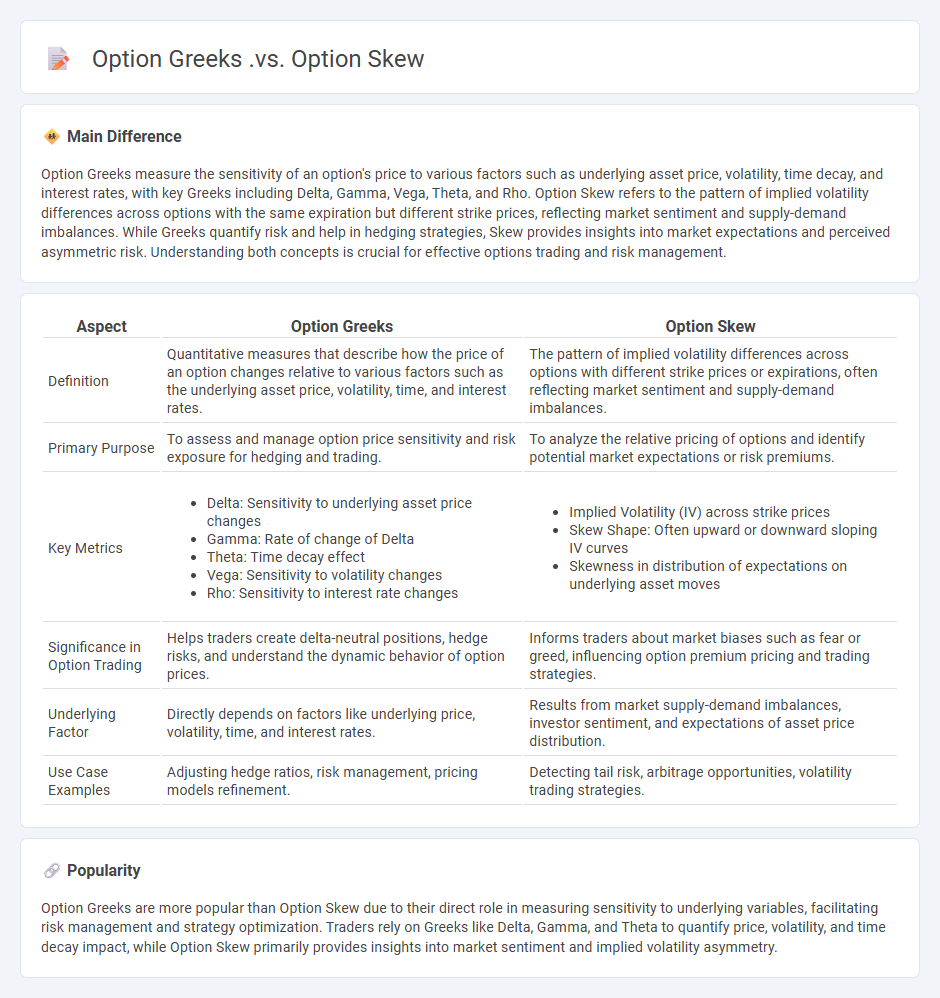
Option Greeks measure the sensitivity of an option's price to various factors such as underlying asset price, volatility, time decay, and interest rates, with key Greeks including Delta, Gamma, Vega, Theta, and Rho. Option Skew refers to the pattern of implied volatility differences across options with the same expiration but different strike prices, reflecting market sentiment and supply-demand imbalances. While Greeks quantify risk and help in hedging strategies, Skew provides insights into market expectations and perceived asymmetric risk. Understanding both concepts is crucial for effective options trading and risk management.
Connection
Option Greeks such as Delta, Gamma, Vega, and Theta quantify the sensitivity of option prices to various factors like underlying asset price, volatility, and time decay, which directly influence option skew patterns. Option skew, representing the implied volatility differences across strike prices or maturities, reflects market expectations and investor sentiment about volatility and risk asymmetry. Understanding the behavior of Option Greeks helps traders interpret option skew dynamics and develop strategies that capitalize on volatility smiles or smirks in different market conditions.
Comparison Table
| Aspect | Option Greeks | Option Skew |
|---|---|---|
| Definition | Quantitative measures that describe how the price of an option changes relative to various factors such as the underlying asset price, volatility, time, and interest rates. | The pattern of implied volatility differences across options with different strike prices or expirations, often reflecting market sentiment and supply-demand imbalances. |
| Primary Purpose | To assess and manage option price sensitivity and risk exposure for hedging and trading. | To analyze the relative pricing of options and identify potential market expectations or risk premiums. |
| Key Metrics |
|
|
| Significance in Option Trading | Helps traders create delta-neutral positions, hedge risks, and understand the dynamic behavior of option prices. | Informs traders about market biases such as fear or greed, influencing option premium pricing and trading strategies. |
| Underlying Factor | Directly depends on factors like underlying price, volatility, time, and interest rates. | Results from market supply-demand imbalances, investor sentiment, and expectations of asset price distribution. |
| Use Case Examples | Adjusting hedge ratios, risk management, pricing models refinement. | Detecting tail risk, arbitrage opportunities, volatility trading strategies. |
Delta
Delta in finance measures the sensitivity of an option's price to changes in the price of the underlying asset, indicating how much the option's value will move per one-point change in the asset's price. It ranges from 0 to 1 for call options and -1 to 0 for put options, with a delta of 0.5 suggesting a 50% chance the option will expire in the money. Traders use delta to hedge portfolios by balancing positions to reduce risk, known as delta hedging. High delta values imply the option behaves more like the underlying asset, while low delta options exhibit less price responsiveness.
Vega
Vega measures an option's sensitivity to volatility changes in the underlying asset, indicating how much the option's price will change with a 1% change in implied volatility. It plays a crucial role in options pricing models like Black-Scholes and is essential for traders managing volatility risk. Vega is typically higher for at-the-money options and longer expirations, reflecting greater sensitivity to volatility fluctuations. Understanding Vega helps investors optimize hedging strategies and manage portfolio risk amid market uncertainty.
Implied Volatility
Implied volatility represents the market's forecast of a security's future price fluctuations, derived from the prices of options contracts. It plays a critical role in the Black-Scholes and other option pricing models by reflecting expected risk over the option's lifetime. Higher implied volatility typically signals greater uncertainty or potential for sharp price movements in the underlying asset, often influencing traders' decisions on hedging or speculation. Market events, earnings reports, and macroeconomic trends frequently drive changes in implied volatility levels across equities, indices, and commodities.
Skewness (Volatility Skew)
Skewness in finance refers to the asymmetry in the distribution of asset returns, often captured by the volatility skew observed in options markets. Volatility skew reflects the differing implied volatilities for options at various strike prices, typically showing higher implied volatility for out-of-the-money puts compared to calls in equity markets. This pattern signals investor sentiment about potential downside risk or market crashes, influencing the pricing of derivatives and risk management strategies. Traders and risk managers analyze volatility skew to identify market expectations and hedge against asymmetric risks in portfolios.
Risk Management
Risk management in finance involves identifying, assessing, and prioritizing financial risks to minimize potential losses and ensure organizational stability. It employs techniques such as diversification, hedging with derivatives, and value at risk (VaR) analysis to manage market, credit, liquidity, and operational risks. Financial institutions rely heavily on regulatory frameworks like Basel III to maintain adequate capital reserves and control risk exposures. Effective risk management enhances portfolio performance and supports compliance with industry standards and investor expectations.
Source and External Links
## Set 1: Understanding Option GreeksUnderstanding Option Greeks - This webpage provides an overview of the different option Greeks, including Delta, Gamma, Theta, Vega, and Rho, which help traders understand the dynamics of options.
## Set 2: Explaining Option SkewSkew in Implied Volatility - This article discusses the concept of skew in implied volatility, detailing how it affects the pricing and trading strategies of options across different strikes within the same expiration.
## Set 3: Trading with Skew and GreeksWhat is Volatility Skew & How to Trade it - This blog post explains volatility skew and its impact on options trading, highlighting how traders can leverage this concept to make informed decisions alongside understanding option Greeks.
FAQs
What are Option Greeks?
Option Greeks are financial metrics that measure the sensitivity of an option's price to various factors: Delta (price change relative to the underlying asset), Gamma (rate of change of Delta), Theta (time decay), Vega (volatility sensitivity), and Rho (interest rate sensitivity).
What is Option Skew?
Option skew is the variation in implied volatility across options with the same expiration but different strike prices, reflecting market sentiment and perceived risk asymmetry.
How do Option Greeks differ from Option Skew?
Option Greeks measure sensitivities of an option's price to various factors like underlying price, volatility, time decay, and interest rates, while Option Skew represents the pattern of implied volatility differences across strike prices or expirations, reflecting market sentiment and demand imbalances.
Which Option Greeks are most affected by Option Skew?
Implied volatility (Vega) and option price sensitivity to underlying price changes (Delta) are most affected by option skew, with Vega showing variations across strike prices and Delta reflecting adjusted risk profiles due to skewed implied volatilities.
How does Option Skew impact options pricing?
Option skew impacts options pricing by causing implied volatility to vary across strike prices, leading to higher premiums for out-of-the-money puts or calls depending on market sentiment.
Why is understanding both Option Greeks and Option Skew important?
Understanding both Option Greeks and Option Skew is important because Option Greeks quantify sensitivity to factors like price, volatility, and time, while Option Skew reveals market sentiment and implied volatility differences across strike prices, enabling more accurate risk management and strategic option pricing.
How do traders use Option Greeks and Option Skew in strategies?
Traders use Option Greeks--Delta, Gamma, Theta, Vega, and Rho--to measure and manage risk factors like price sensitivity, time decay, and volatility in options strategies, while analyzing Option Skew helps identify implied volatility differences across strikes or expirations to exploit mispriced options and tailor hedging or speculative positions.
 calledges.com
calledges.com