Fixed-point arithmetic uses a set number of digits after the decimal point, offering faster computation and reduced resource consumption in embedded systems and digital signal processing. Floating-point arithmetic provides a wider dynamic range and higher precision by representing numbers with significant and exponent parts, making it essential in scientific calculations and graphics. Explore the differences to understand their impact on performance and accuracy in various applications.
Main Difference
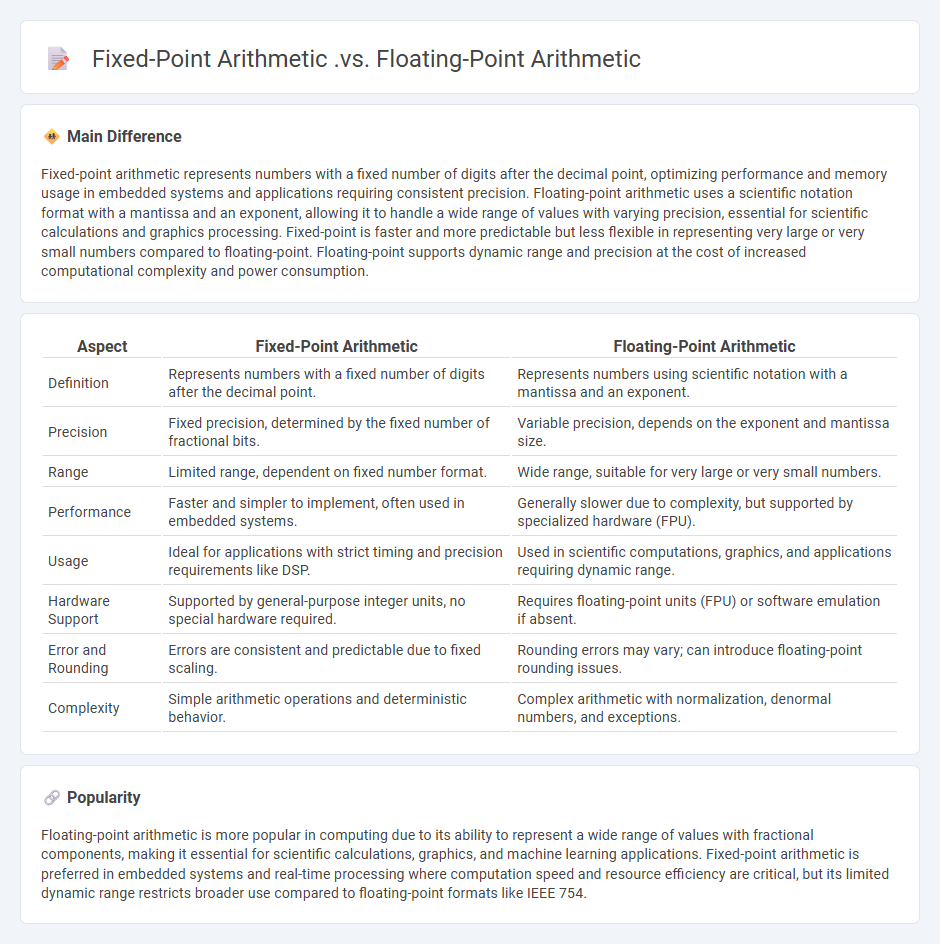
Fixed-point arithmetic represents numbers with a fixed number of digits after the decimal point, optimizing performance and memory usage in embedded systems and applications requiring consistent precision. Floating-point arithmetic uses a scientific notation format with a mantissa and an exponent, allowing it to handle a wide range of values with varying precision, essential for scientific calculations and graphics processing. Fixed-point is faster and more predictable but less flexible in representing very large or very small numbers compared to floating-point. Floating-point supports dynamic range and precision at the cost of increased computational complexity and power consumption.
Connection
Fixed-point arithmetic and floating-point arithmetic are both methods for representing real numbers in computer systems, with fixed-point using a fixed number of digits after the decimal point and floating-point representing numbers with a mantissa and exponent for a wider dynamic range. Fixed-point arithmetic is often used in embedded systems and digital signal processing where performance and resource constraints require efficient, low-overhead operations. Floating-point arithmetic, standardized by IEEE 754, enables higher precision and range suitable for scientific computing and applications needing complex numerical calculations.
Comparison Table
| Aspect | Fixed-Point Arithmetic | Floating-Point Arithmetic |
|---|---|---|
| Definition | Represents numbers with a fixed number of digits after the decimal point. | Represents numbers using scientific notation with a mantissa and an exponent. |
| Precision | Fixed precision, determined by the fixed number of fractional bits. | Variable precision, depends on the exponent and mantissa size. |
| Range | Limited range, dependent on fixed number format. | Wide range, suitable for very large or very small numbers. |
| Performance | Faster and simpler to implement, often used in embedded systems. | Generally slower due to complexity, but supported by specialized hardware (FPU). |
| Usage | Ideal for applications with strict timing and precision requirements like DSP. | Used in scientific computations, graphics, and applications requiring dynamic range. |
| Hardware Support | Supported by general-purpose integer units, no special hardware required. | Requires floating-point units (FPU) or software emulation if absent. |
| Error and Rounding | Errors are consistent and predictable due to fixed scaling. | Rounding errors may vary; can introduce floating-point rounding issues. |
| Complexity | Simple arithmetic operations and deterministic behavior. | Complex arithmetic with normalization, denormal numbers, and exceptions. |
Precision
Precision in computing refers to the level of detail and exactness with which data is represented and processed, particularly in numerical computations. It involves the number of bits used to store a value, influencing the accuracy and range of representable numbers, such as in floating-point arithmetic where single precision typically uses 32 bits and double precision uses 64 bits. Higher precision reduces rounding errors in calculations, critical for scientific simulations, financial models, and machine learning algorithms. Processor architectures and programming languages provide explicit data types to manage precision for optimal performance and accuracy.
Range
In computing, range refers to the set of all possible values that a variable or data type can hold, often determined by its bit width and representation format. For example, a signed 32-bit integer has a range from -2,147,483,648 to 2,147,483,647. Floating-point numbers follow the IEEE 754 standard, with single precision providing a range roughly between 1.4 x 10^-45 and 3.4 x 10^38. Understanding these ranges is critical to preventing overflow errors and ensuring data integrity in software development.
Memory Efficiency
Memory efficiency in computers refers to optimizing the usage of RAM and storage to maximize system performance while minimizing resource consumption. Techniques such as memory compression, efficient garbage collection, and optimized data structures reduce memory overhead and improve processing speed. Modern operating systems like Windows 11 and macOS Ventura implement advanced memory management algorithms to allocate resources dynamically and prevent fragmentation. Ensuring high memory efficiency is critical for running complex applications, virtual machines, and large-scale data analysis without hardware upgrades.
Computation Speed
Computation speed in computers is measured by the number of instructions a processor can execute per second, commonly expressed in gigahertz (GHz) or millions of instructions per second (MIPS). Modern CPUs, such as those based on Intel Core i9 or AMD Ryzen 9 architectures, achieve speeds exceeding 5 GHz with multiple cores enabling parallel processing. The speed significantly impacts performance in tasks like data analysis, gaming, and scientific simulations. Advances in semiconductor technology, including smaller transistor sizes and improved thermal management, continue to enhance computation speeds.
Application Suitability
Application suitability in computer systems refers to how well software or hardware aligns with the specific requirements and constraints of a given computing environment. Factors such as compatibility with operating systems, hardware specifications, intended use cases, and user needs determine the appropriateness of applications. Evaluating performance metrics like processing speed, memory usage, and scalability is essential to ensure optimal efficiency. Proper application suitability enhances system reliability, user satisfaction, and overall productivity in computing tasks.
Source and External Links
Fixed-Point vs. Floating-Point Digital Signal Processing - Floating-point arithmetic supports a much wider dynamic range and can represent very small and very large numbers due to its variable decimal point, while fixed-point represents numbers with a fixed number of digits after the decimal point, yielding higher precision within a limited range but less flexibility.
Floating-point or fixed-point: a choice between precision and efficiency - Fixed-point arithmetic operations can be more efficient, requiring fewer cycles and less power for some operations such as addition, but require prior knowledge of variable magnitudes and can trade off accuracy for execution time.
Fixed-point arithmetic - Wikipedia - Fixed-point computations are often faster and more hardware-efficient than floating-point, especially on embedded systems without FPUs, and can offer better precision for limited known ranges, whereas floating-point offers greater range and standardized numeric representation.
FAQs
What is fixed-point arithmetic?
Fixed-point arithmetic is a numerical representation and computation method where numbers have a fixed number of digits after the decimal point, enabling efficient and precise calculations in systems with limited hardware resources or real-time constraints.
What is floating-point arithmetic?
Floating-point arithmetic is a method of representing and performing calculations on real numbers using a format that approximates values with a fixed number of significant digits and an exponent.
How do fixed-point and floating-point arithmetic differ?
Fixed-point arithmetic represents numbers with a fixed number of digits before and after the decimal, ideal for consistent precision and faster computation in embedded systems. Floating-point arithmetic uses scientific notation with a mantissa and exponent, allowing a wide range of values and dynamic precision, essential for complex calculations in scientific computing and graphics.
What are the advantages of fixed-point arithmetic?
Fixed-point arithmetic offers faster computation, lower hardware complexity, reduced power consumption, and deterministic precision ideal for embedded systems and real-time applications.
What are the benefits of floating-point arithmetic?
Floating-point arithmetic enables precise representation of very large or very small numbers, supports a wide dynamic range, allows efficient scientific and engineering calculations, and facilitates standardized computation across different hardware platforms.
In which applications is fixed-point preferred over floating-point?
Fixed-point is preferred over floating-point in embedded systems, digital signal processing (DSP), real-time control systems, and low-power or resource-constrained devices due to its lower computational complexity, reduced memory usage, faster arithmetic operations, and minimized hardware cost.
What are the main limitations of floating-point arithmetic?
Floating-point arithmetic is limited by rounding errors, finite precision, representation of very large or small numbers leading to overflow or underflow, loss of associativity, and inability to represent some decimal fractions exactly.
 calledges.com
calledges.com