Duration measures the sensitivity of a bond's price to changes in interest rates, calculating the weighted average time to receive cash flows. Convexity enhances this by accounting for the curvature in the price-yield relationship, providing a more accurate estimate of price changes for larger interest rate movements. Explore how Duration and Convexity together improve bond risk management strategies.
Main Difference
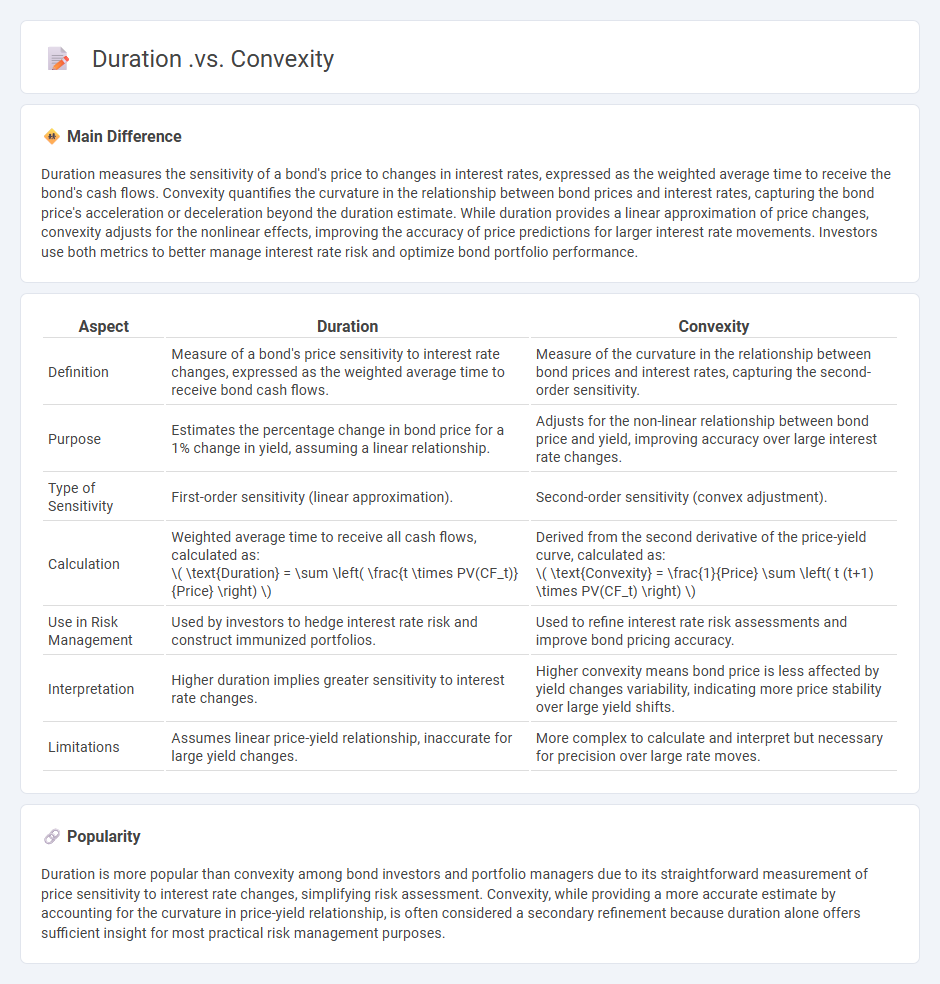
Duration measures the sensitivity of a bond's price to changes in interest rates, expressed as the weighted average time to receive the bond's cash flows. Convexity quantifies the curvature in the relationship between bond prices and interest rates, capturing the bond price's acceleration or deceleration beyond the duration estimate. While duration provides a linear approximation of price changes, convexity adjusts for the nonlinear effects, improving the accuracy of price predictions for larger interest rate movements. Investors use both metrics to better manage interest rate risk and optimize bond portfolio performance.
Connection
Duration measures a bond's sensitivity to interest rate changes by estimating the weighted average time until cash flows are received. Convexity refines this measurement by accounting for the curvature in the price-yield relationship, improving the accuracy of bond price predictions under varying interest rates. Together, duration and convexity provide a comprehensive framework for assessing interest rate risk and bond price volatility.
Comparison Table
| Aspect | Duration | Convexity |
|---|---|---|
| Definition | Measure of a bond's price sensitivity to interest rate changes, expressed as the weighted average time to receive bond cash flows. | Measure of the curvature in the relationship between bond prices and interest rates, capturing the second-order sensitivity. |
| Purpose | Estimates the percentage change in bond price for a 1% change in yield, assuming a linear relationship. | Adjusts for the non-linear relationship between bond price and yield, improving accuracy over large interest rate changes. |
| Type of Sensitivity | First-order sensitivity (linear approximation). | Second-order sensitivity (convex adjustment). |
| Calculation |
Weighted average time to receive all cash flows, calculated as:
\( \text{Duration} = \sum \left( \frac{t \times PV(CF_t)}{Price} \right) \) |
Derived from the second derivative of the price-yield curve, calculated as:
\( \text{Convexity} = \frac{1}{Price} \sum \left( t (t+1) \times PV(CF_t) \right) \) |
| Use in Risk Management | Used by investors to hedge interest rate risk and construct immunized portfolios. | Used to refine interest rate risk assessments and improve bond pricing accuracy. |
| Interpretation | Higher duration implies greater sensitivity to interest rate changes. | Higher convexity means bond price is less affected by yield changes variability, indicating more price stability over large yield shifts. |
| Limitations | Assumes linear price-yield relationship, inaccurate for large yield changes. | More complex to calculate and interpret but necessary for precision over large rate moves. |
Interest Rate Sensitivity
Interest rate sensitivity measures how the value of financial assets, such as bonds or loans, responds to changes in prevailing interest rates. Bonds with longer durations typically exhibit higher interest rate sensitivity, meaning their prices fluctuate more when rates shift. This concept is crucial for portfolio management and risk assessment in fixed-income investments. Understanding interest rate sensitivity helps investors anticipate potential losses or gains in response to monetary policy changes by central banks.
Price Volatility
Price volatility in finance refers to the degree of variation in the price of a financial instrument over time, measured by statistical metrics such as standard deviation or variance. High volatility indicates large price swings, often associated with increased market risk and trading opportunities, while low volatility suggests more stable prices. Factors influencing volatility include economic events, market sentiment, geopolitical developments, and liquidity conditions. Volatility indexes like the VIX provide investors with insights into expected market fluctuations and risk levels.
Linear Relationship (Duration)
Linear relationships in financial duration analysis measure the sensitivity of bond prices to interest rate changes, often represented by the first derivative of the price-yield curve. Duration quantifies the weighted average time to receive a bond's cash flows, with Macaulay and modified duration being key metrics used by investors and risk managers. A linear approximation assumes small interest rate shifts, allowing for quick estimation of price changes through duration multiplied by yield changes. This method assists in portfolio immunization and interest rate risk management in fixed income investment strategies.
Curvature Effect (Convexity)
Convexity measures the curvature effect in bond pricing, reflecting how the duration changes as interest rates fluctuate. This metric enhances the accuracy of price estimations by accounting for the nonlinear relationship between bond prices and yields. Investors use convexity to assess interest rate risk and improve portfolio immunization strategies. Higher convexity indicates greater sensitivity of bond prices to interest rate movements, which is crucial for managing fixed-income securities.
Risk Management
Risk management in finance involves identifying, assessing, and prioritizing potential financial risks to minimize losses and maximize returns. Techniques like diversification, hedging with derivatives, and insurance are commonly used to mitigate risks in investment portfolios and corporate finance. Quantitative models such as Value at Risk (VaR) and stress testing help estimate potential losses under adverse market conditions. Effective risk management supports regulatory compliance and enhances decision-making in financial institutions and investment firms.
Source and External Links
## Set 1: Academic ViewRelative Impact of Duration and Convexity on Bond Price Changes - This paper explores the mathematical relationship between duration and convexity in bond price changes, highlighting their relative importance in different scenarios.
## Set 2: Financial AnalysisDuration and Convexity in Bond market - Macro Hive - This article covers the concepts of duration and convexity in bond markets, focusing on how they help predict bond price changes and their practical applications.
## Set 3: Investment PerspectiveDuration & Convexity - Fixed Income Bond Basics | Raymond James - This resource provides an overview of duration and convexity from an investment perspective, explaining how they impact bond prices and investor strategies.
FAQs
What is bond duration?
Bond duration measures the sensitivity of a bond's price to changes in interest rates, expressed in years, indicating the weighted average time to receive all bond payments.
What is bond convexity?
Bond convexity measures the curvature in the relationship between bond prices and yields, reflecting how much a bond's duration changes as interest rates fluctuate.
How do duration and convexity differ?
Duration measures a bond's sensitivity to interest rate changes by estimating the percentage price change for a 1% change in yield, while convexity measures the curvature of the price-yield relationship, capturing how duration changes as yields change, providing a more accurate estimate of price sensitivity for larger interest rate movements.
Why is duration important for investors?
Duration measures a bond's sensitivity to interest rate changes, helping investors assess risk and manage portfolio volatility effectively.
When does convexity become more relevant than duration?
Convexity becomes more relevant than duration when bond price sensitivity to interest rate changes is nonlinear, especially for large interest rate shifts or bonds with embedded options.
How do interest rates affect duration and convexity?
Higher interest rates decrease bond duration by reducing the present value of future cash flows and increase convexity by amplifying the curvature of price-yield relationship.
How can investors use duration and convexity to manage risk?
Investors use duration to measure a bond's sensitivity to interest rate changes, guiding portfolio adjustments to interest rate risk. They apply convexity to account for the curvature of price-yield relationship, improving accuracy in estimating bond price changes for large interest rate movements and enhancing risk management strategies.
 calledges.com
calledges.com