Put-call parity establishes a fundamental relationship between the prices of European put and call options with the same strike price and expiration date, ensuring no arbitrage opportunities in efficient markets. Put-call symmetry explores the conceptual and structural similarities between put and call options, highlighting how their payoffs and market behaviors mirror each other under certain conditions. Discover more about how these concepts influence options pricing and trading strategies.
Main Difference
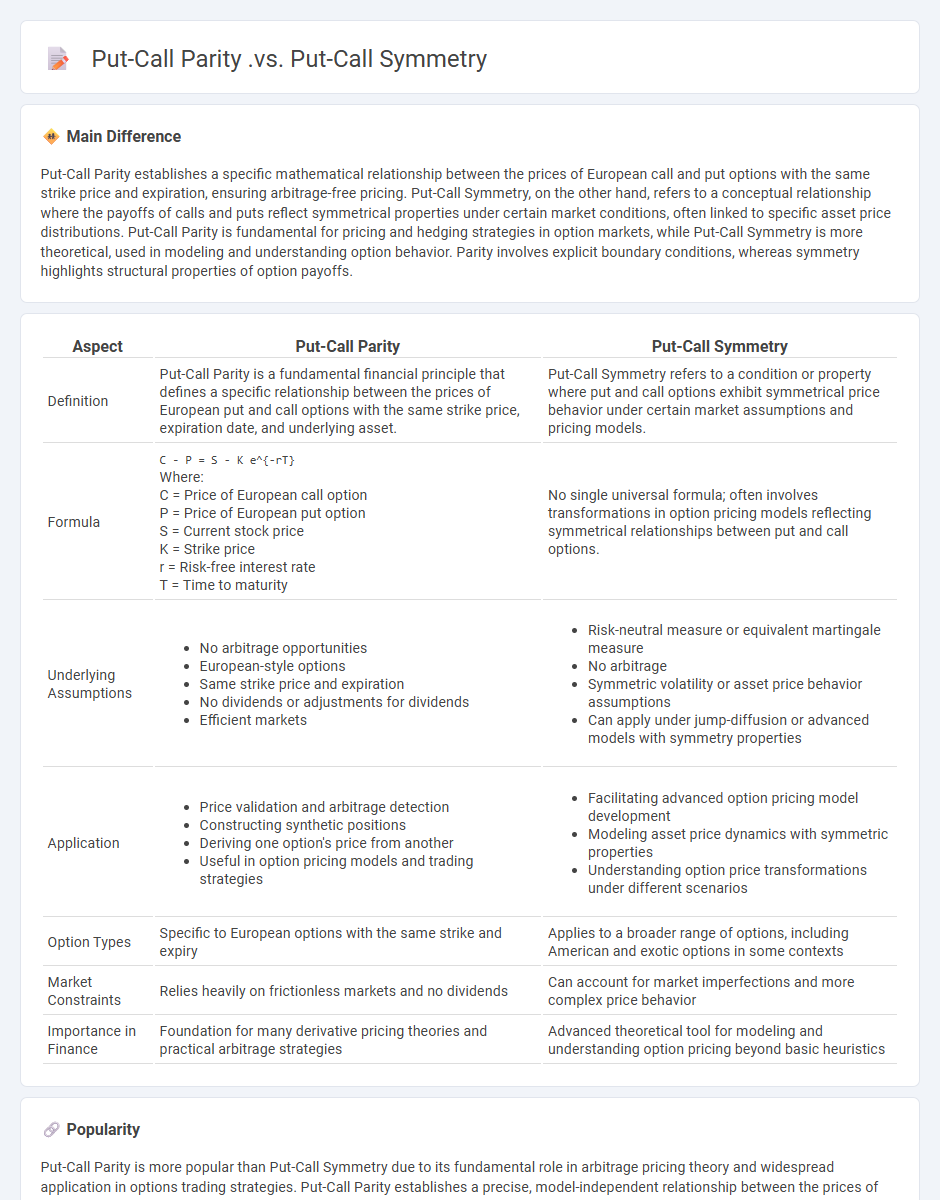
Put-Call Parity establishes a specific mathematical relationship between the prices of European call and put options with the same strike price and expiration, ensuring arbitrage-free pricing. Put-Call Symmetry, on the other hand, refers to a conceptual relationship where the payoffs of calls and puts reflect symmetrical properties under certain market conditions, often linked to specific asset price distributions. Put-Call Parity is fundamental for pricing and hedging strategies in option markets, while Put-Call Symmetry is more theoretical, used in modeling and understanding option behavior. Parity involves explicit boundary conditions, whereas symmetry highlights structural properties of option payoffs.
Connection
Put-Call Parity establishes a fundamental equilibrium relationship between the prices of European call and put options with the same strike price and expiration date, ensuring no arbitrage opportunities exist. Put-Call Symmetry extends this concept by highlighting conditions under which the distributions of underlying asset prices make call and put options equivalent in value when adjusted for strike prices and dividends. Both principles are interconnected through their reliance on no-arbitrage conditions and pricing models like the Black-Scholes framework to maintain consistent and fair option valuations.
Comparison Table
| Aspect | Put-Call Parity | Put-Call Symmetry |
|---|---|---|
| Definition | Put-Call Parity is a fundamental financial principle that defines a specific relationship between the prices of European put and call options with the same strike price, expiration date, and underlying asset. | Put-Call Symmetry refers to a condition or property where put and call options exhibit symmetrical price behavior under certain market assumptions and pricing models. |
| Formula |
C - P = S - K e^{-rT}Where: C = Price of European call option P = Price of European put option S = Current stock price K = Strike price r = Risk-free interest rate T = Time to maturity |
No single universal formula; often involves transformations in option pricing models reflecting symmetrical relationships between put and call options. |
| Underlying Assumptions |
|
|
| Application |
|
|
| Option Types | Specific to European options with the same strike and expiry | Applies to a broader range of options, including American and exotic options in some contexts |
| Market Constraints | Relies heavily on frictionless markets and no dividends | Can account for market imperfections and more complex price behavior |
| Importance in Finance | Foundation for many derivative pricing theories and practical arbitrage strategies | Advanced theoretical tool for modeling and understanding option pricing beyond basic heuristics |
Arbitrage
Arbitrage in finance involves the simultaneous purchase and sale of an asset to profit from price discrepancies across different markets. This practice ensures market efficiency by correcting price differences, thus aligning asset values globally. High-frequency trading firms often use sophisticated algorithms to exploit these arbitrage opportunities in stocks, currencies, and commodities. Regulatory frameworks monitor arbitrage activities to prevent market manipulation and ensure fair trading conditions.
European Options
European options grant the holder the right to buy or sell an underlying asset exclusively at the predetermined strike price on the option's expiration date. These derivatives are primarily used in equity, currency, and index markets, facilitating hedging and speculative strategies. The Black-Scholes model is commonly applied to assess their fair value, capitalizing on assumptions like constant volatility and risk-free interest rates. Liquidity and pricing efficiency for European options are especially notable on major exchanges such as the Chicago Board Options Exchange (CBOE) and Eurex.
Strike Price
The strike price in finance refers to the predetermined price at which an option holder can buy or sell the underlying asset. It plays a crucial role in determining an option's intrinsic value and profitability at expiration. For example, a call option with a strike price of $50 allows the holder to purchase the underlying stock at $50 regardless of the current market price. Accurate strike price selection is essential for options traders seeking to maximize returns or hedge risk effectively.
Underlying Asset
An underlying asset in finance refers to the financial instrument or asset on which a derivative's price is based, such as stocks, bonds, commodities, currencies, or market indexes. These assets serve as the foundation for derivative contracts like options, futures, and swaps, determining their value through market movements. The performance and price fluctuations of the underlying asset directly affect the derivative's payoff and risk profile. Accurate valuation of the underlying asset is crucial for pricing derivatives and managing associated financial risks effectively.
Payoff Structure
The payoff structure in finance defines the set of potential outcomes and corresponding monetary gains or losses from an investment or financial instrument. It represents how the value or return changes based on the underlying asset's performance, often visualized through graphs for options, futures, and other derivatives. Understanding the payoff structure is crucial for evaluating risk exposure and potential profit scenarios in trading strategies. Examples include the linear payoff of stocks, the asymmetric payoff of call and put options, and the limited loss profiles of options sellers.
Source and External Links
The Put-Call Symmetry (PCS) in Layman's terms... - Finance Tutoring - Put-Call Symmetry relates prices of European puts and calls with different strike prices connected through the forward price of the underlying, requiring frictionless markets, no arbitrage, zero drift, and symmetric returns assumptions.
Put-call parity - Wikipedia - Put-Call Parity defines a relationship between European call and put options with the same strike price and expiry, showing that a portfolio of a long call and short put equals a forward contract, under no-arbitrage and frictionless market assumptions.
Put-Call Symmetry: Extensions and Applications - Put-Call Symmetry extends the classic relationship between calls and puts at strikes logarithmically equidistant to the forward price, and generalizes to advanced volatility models and asymmetric dynamics, enabling semi-static hedging strategies.
FAQs
What is put-call parity?
Put-call parity is a financial principle establishing that the price difference between a European call option and a European put option on the same asset, strike price, and expiration date equals the present value of the strike price minus the asset's current price.
What is put-call symmetry?
Put-call symmetry is a financial principle stating that under certain conditions, the prices of European call and put options with the same strike price and expiration date can be derived from each other using a specific mathematical relationship involving the underlying asset price, strike price, risk-free interest rate, and time to maturity.
How do put-call parity and put-call symmetry differ?
Put-call parity defines a specific arbitrage relationship between European call and put options with the same strike price and expiration, expressed as C - P = S - K e^(-rT). Put-call symmetry generalizes this concept, relating the prices of calls and puts under different market conditions or option styles, often involving adjustments for dividends, American options, or stochastic interest rates.
Why is put-call parity important in options pricing?
Put-call parity is important in options pricing because it ensures arbitrage-free pricing by establishing a precise relationship between the prices of European call and put options with the same strike price and expiration date.
How is put-call symmetry used in financial markets?
Put-call symmetry is used in financial markets to price options by exploiting the relationship between put and call prices with the same strike price and expiration, enabling arbitrage opportunities and improving market efficiency.
What assumptions are needed for put-call parity to hold?
Put-call parity holds under assumptions of no arbitrage, European-style options, identical strike prices and expiration dates for call and put, frictionless markets without transaction costs or taxes, ability to short-sell underlying assets, and constant risk-free interest rates.
Can market inefficiencies affect put-call symmetry?
Market inefficiencies such as liquidity constraints, transaction costs, and information asymmetry can disrupt put-call symmetry by causing deviations from the theoretical parity relationships in options pricing.
 calledges.com
calledges.com