Monte Carlo simulation generates numerous random samples to model the probability of different outcomes in complex systems, relying on computational algorithms to analyze risk and uncertainty. Bootstrapping resamples observed data with replacement to estimate the distribution of a statistic, focusing on empirical data without assuming a specific theoretical distribution. Explore these powerful techniques to enhance your understanding of statistical modeling and decision-making processes.
Main Difference
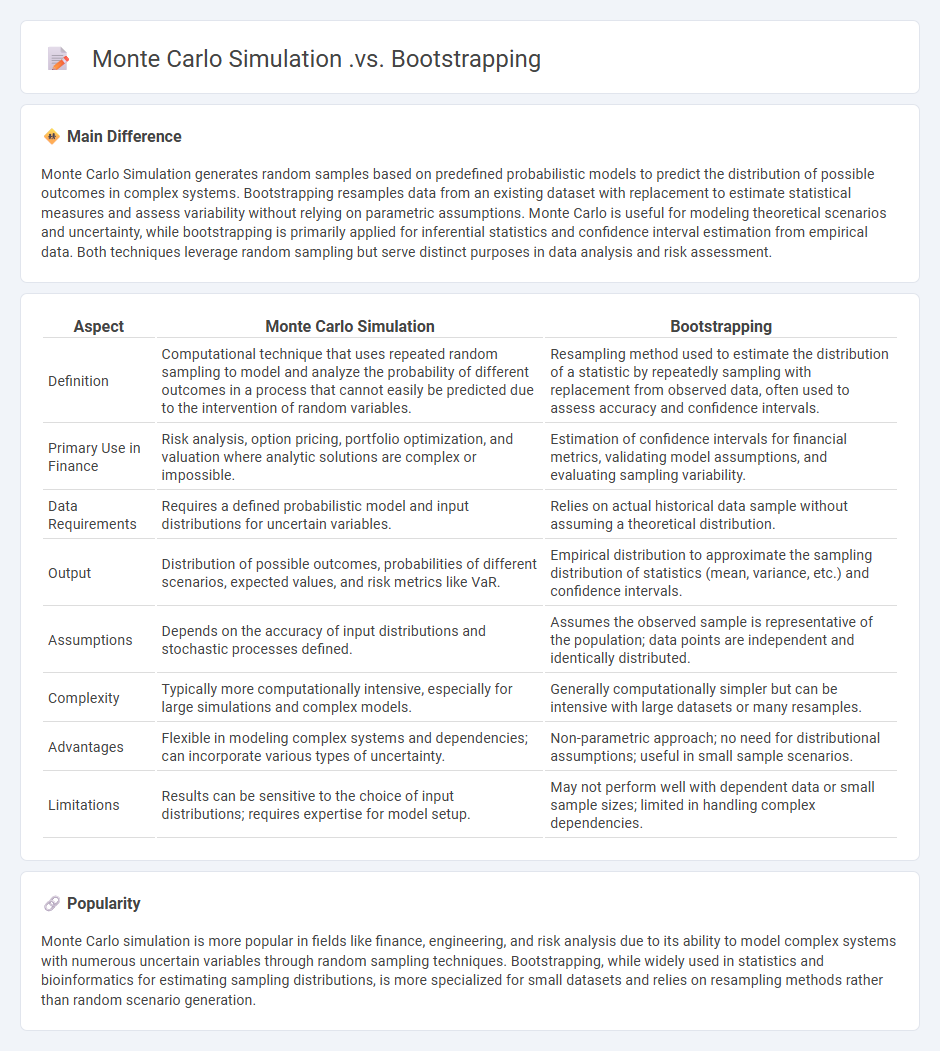
Monte Carlo Simulation generates random samples based on predefined probabilistic models to predict the distribution of possible outcomes in complex systems. Bootstrapping resamples data from an existing dataset with replacement to estimate statistical measures and assess variability without relying on parametric assumptions. Monte Carlo is useful for modeling theoretical scenarios and uncertainty, while bootstrapping is primarily applied for inferential statistics and confidence interval estimation from empirical data. Both techniques leverage random sampling but serve distinct purposes in data analysis and risk assessment.
Connection
Monte Carlo Simulation and Bootstrapping are connected through their reliance on random sampling to estimate statistical properties. Both methods generate multiple simulated datasets to analyze variability and uncertainty in model predictions or parameter estimates. Monte Carlo Simulation typically uses known probability distributions, while Bootstrapping resamples observed data to create empirical distributions without strict distributional assumptions.
Comparison Table
| Aspect | Monte Carlo Simulation | Bootstrapping |
|---|---|---|
| Definition | Computational technique that uses repeated random sampling to model and analyze the probability of different outcomes in a process that cannot easily be predicted due to the intervention of random variables. | Resampling method used to estimate the distribution of a statistic by repeatedly sampling with replacement from observed data, often used to assess accuracy and confidence intervals. |
| Primary Use in Finance | Risk analysis, option pricing, portfolio optimization, and valuation where analytic solutions are complex or impossible. | Estimation of confidence intervals for financial metrics, validating model assumptions, and evaluating sampling variability. |
| Data Requirements | Requires a defined probabilistic model and input distributions for uncertain variables. | Relies on actual historical data sample without assuming a theoretical distribution. |
| Output | Distribution of possible outcomes, probabilities of different scenarios, expected values, and risk metrics like VaR. | Empirical distribution to approximate the sampling distribution of statistics (mean, variance, etc.) and confidence intervals. |
| Assumptions | Depends on the accuracy of input distributions and stochastic processes defined. | Assumes the observed sample is representative of the population; data points are independent and identically distributed. |
| Complexity | Typically more computationally intensive, especially for large simulations and complex models. | Generally computationally simpler but can be intensive with large datasets or many resamples. |
| Advantages | Flexible in modeling complex systems and dependencies; can incorporate various types of uncertainty. | Non-parametric approach; no need for distributional assumptions; useful in small sample scenarios. |
| Limitations | Results can be sensitive to the choice of input distributions; requires expertise for model setup. | May not perform well with dependent data or small sample sizes; limited in handling complex dependencies. |
Probability Distribution Modeling
Probability distribution modeling in finance quantifies the likelihood of different financial outcomes by representing uncertain variables like asset returns or market risks. Commonly used distributions include the Normal distribution for asset returns, the Log-normal distribution for stock prices, and the Poisson distribution for modeling rare events. Accurate modeling informs risk management, option pricing, and portfolio optimization by capturing the probabilistic behavior of financial instruments. Advanced techniques such as Monte Carlo simulation and Bayesian inference enhance model precision and adaptability.
Resampling Techniques
Resampling techniques in finance enhance portfolio optimization by addressing estimation errors in asset returns and covariances. Methods such as bootstrap resampling generate multiple simulated datasets to improve the robustness of risk and return estimates. This approach reduces overfitting and volatility in portfolio weights, leading to more stable and reliable investment strategies. Resampling has been shown to outperform traditional Markowitz optimization, especially in markets with limited historical data.
Risk Assessment
Risk assessment in finance involves identifying, analyzing, and quantifying potential financial losses associated with investments, loans, or portfolios. Key methodologies include Value at Risk (VaR), stress testing, and scenario analysis to evaluate market, credit, and operational risks. Financial institutions utilize risk models and historical data to establish risk-adjusted returns and regulatory capital requirements. Accurate risk assessment supports informed decision-making, promotes financial stability, and ensures compliance with Basel III and IFRS 9 standards.
Path Dependency
Path dependency in finance refers to the phenomenon where the outcomes of financial decisions or market behaviors are influenced by the historical sequence of events, rather than solely by current conditions. This concept is critical in asset pricing models, especially in the valuation of path-dependent options like Asian options, where the payoff depends on the average price of the underlying asset over time. Portfolio management strategies often incorporate path dependency when evaluating the impact of past market movements on future asset allocation and risk assessment. Understanding path dependency helps in modeling financial markets more accurately, capturing the persistence and momentum effects observed in empirical data.
Scenario Analysis
Scenario analysis in finance evaluates potential outcomes by modeling multiple economic conditions to assess portfolio risks and returns. It incorporates variables such as interest rates, inflation, and market volatility to project financial performance under different scenarios. Financial institutions utilize this technique to stress-test investments and ensure regulatory compliance like Basel III requirements. This method enhances decision-making by quantifying potential losses and gains in uncertain market environments.
Source and External Links
Statistical Bootstrapping and Monte Carlo Simulation - This webpage compares bootstrapping and Monte Carlo simulation, highlighting that bootstrapping generates demand scenarios for forecasting, while Monte Carlo simulation uses these scenarios for inventory optimization.
Monte Carlo Simulations and Bootstrap - This document explains the bootstrap as a Monte Carlo simulation approach used to estimate the uncertainty of a statistic by resampling from the original data.
Monte Carlo and Bootstrap Methods - This lecture material discusses the use of Monte Carlo methods and bootstrapping in statistics, focusing on their applications in estimating functions and uncertainties.
FAQs
What is Monte Carlo simulation?
Monte Carlo simulation is a computational technique that uses random sampling and statistical modeling to estimate probabilities and analyze complex systems or processes.
What is bootstrapping in statistics?
Bootstrapping in statistics is a resampling method that involves repeatedly drawing samples with replacement from an original dataset to estimate the sampling distribution of a statistic.
How do Monte Carlo simulation and bootstrapping differ?
Monte Carlo simulation uses random sampling to model and analyze complex systems based on known probability distributions, while bootstrapping resamples observed data with replacement to estimate the sampling distribution and assess the accuracy of sample statistics.
What are the main uses of Monte Carlo simulation?
Monte Carlo simulation is mainly used for risk assessment, financial forecasting, project management, decision analysis, and optimization in fields such as finance, engineering, and supply chain management.
How does bootstrapping work in data analysis?
Bootstrapping in data analysis works by repeatedly sampling with replacement from the original dataset to create multiple simulated samples, enabling estimation of statistical properties like confidence intervals and variance without relying on strict parametric assumptions.
What are the advantages of Monte Carlo simulation over bootstrapping?
Monte Carlo simulation offers advantages over bootstrapping by allowing modeling of complex stochastic processes based on specified probability distributions, enabling scenario analysis and forecasting beyond the original data, while bootstrapping relies solely on resampling observed data without assuming underlying distributions.
When should you use bootstrapping instead of Monte Carlo simulation?
Use bootstrapping instead of Monte Carlo simulation when you have limited data and want to estimate the sampling distribution of a statistic by resampling the observed dataset without assuming an underlying probability distribution.
 calledges.com
calledges.com