Effective Annual Rate (EAR) accurately reflects the true annual cost of borrowing or the real yield on an investment by accounting for compound interest within a year. Annual Percentage Rate (APR) represents the annualized interest rate without compounding, often used to compare loan costs and credit products. Explore more to understand how EAR and APR impact financial decisions and which metric suits your needs.
Main Difference
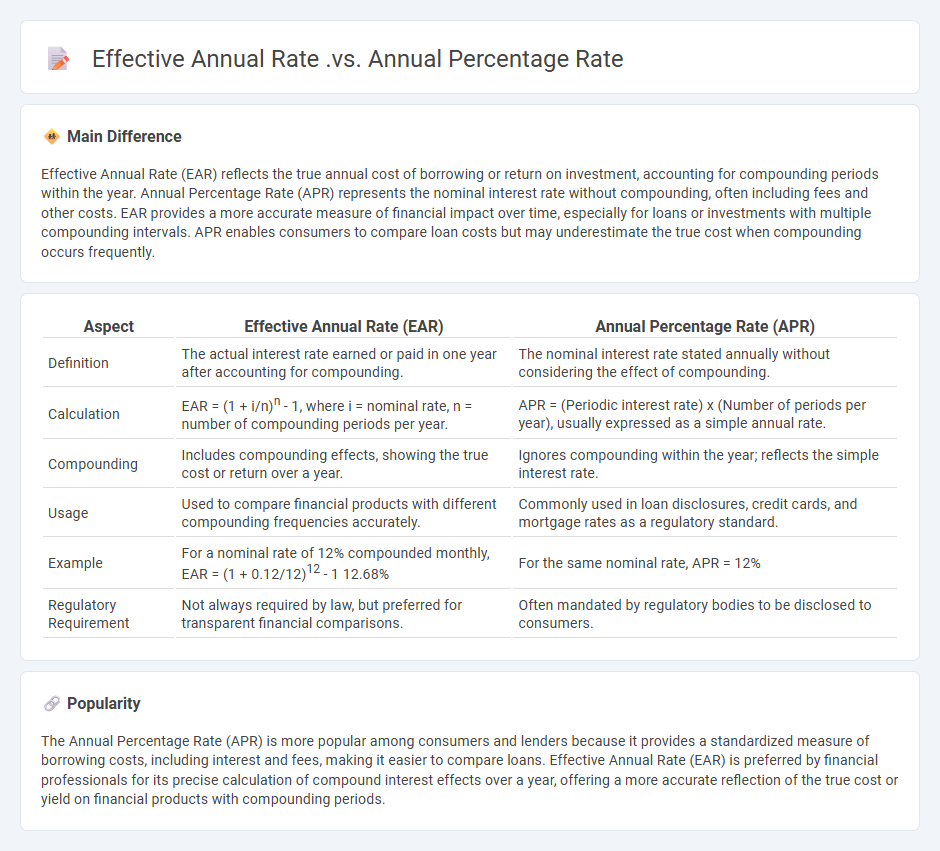
Effective Annual Rate (EAR) reflects the true annual cost of borrowing or return on investment, accounting for compounding periods within the year. Annual Percentage Rate (APR) represents the nominal interest rate without compounding, often including fees and other costs. EAR provides a more accurate measure of financial impact over time, especially for loans or investments with multiple compounding intervals. APR enables consumers to compare loan costs but may underestimate the true cost when compounding occurs frequently.
Connection
Effective Annual Rate (EAR) reflects the actual interest earned or paid on an investment or loan over a year, accounting for compounding periods. Annual Percentage Rate (APR) represents the annualized interest rate without considering intra-year compounding, often used to compare loan costs. EAR can be derived from APR by incorporating the frequency of compounding, making EAR a more accurate measure of the true annual cost or return.
Comparison Table
| Aspect | Effective Annual Rate (EAR) | Annual Percentage Rate (APR) |
|---|---|---|
| Definition | The actual interest rate earned or paid in one year after accounting for compounding. | The nominal interest rate stated annually without considering the effect of compounding. |
| Calculation | EAR = (1 + i/n)n - 1, where i = nominal rate, n = number of compounding periods per year. | APR = (Periodic interest rate) x (Number of periods per year), usually expressed as a simple annual rate. |
| Compounding | Includes compounding effects, showing the true cost or return over a year. | Ignores compounding within the year; reflects the simple interest rate. |
| Usage | Used to compare financial products with different compounding frequencies accurately. | Commonly used in loan disclosures, credit cards, and mortgage rates as a regulatory standard. |
| Example | For a nominal rate of 12% compounded monthly, EAR = (1 + 0.12/12)12 - 1 12.68% | For the same nominal rate, APR = 12% |
| Regulatory Requirement | Not always required by law, but preferred for transparent financial comparisons. | Often mandated by regulatory bodies to be disclosed to consumers. |
Compounding Frequency
Compounding frequency in finance refers to the number of times interest is calculated and added to the principal balance within a specific period, typically a year. Common compounding intervals include annual, semi-annual, quarterly, monthly, and daily, with more frequent compounding resulting in higher effective yields. Financial instruments like savings accounts, bonds, and loans often specify the compounding frequency, influencing the total amount accrued or owed. Understanding the impact of compounding frequency is crucial for accurate interest calculations and investment growth projections.
Nominal Interest Rate
The nominal interest rate represents the percentage increase in money that a borrower pays to a lender, not adjusted for inflation. It is commonly expressed on an annual basis and influences various financial instruments such as loans, bonds, and savings accounts. Investors and analysts use the nominal rate to estimate future cash flows, but real returns require adjusting for inflation. Central banks often manipulate nominal interest rates through monetary policy to control economic growth and inflation levels.
Effective Annual Rate (EAR)
Effective Annual Rate (EAR) represents the true annual interest earned or paid on an investment or loan, accounting for compounding periods within the year. It is calculated using the formula EAR = (1 + i/n)n - 1, where i is the nominal interest rate and n is the number of compounding periods per year. EAR provides a consistent basis for comparing interest rates with different compounding frequencies, such as monthly, quarterly, or daily. Financial institutions often use EAR to disclose interest rates on savings accounts, bonds, and loans for transparent and accurate cost or return assessment.
Annual Percentage Rate (APR)
Annual Percentage Rate (APR) quantifies the yearly cost of borrowing, expressed as a percentage that includes interest rates and additional fees. This standardized metric enables consumers to compare loan offers, credit cards, and mortgages effectively by reflecting the true cost over a one-year period. Financial institutions typically calculate APR using a formula mandated by regulatory bodies such as the Truth in Lending Act (TILA) in the United States. APR variations depend on loan type, borrower creditworthiness, and market interest rates, influencing overall repayment amounts and financial planning.
Interest Calculation
Interest calculation in finance involves determining the cost of borrowing or the earnings from invested capital over time. It primarily relies on principal, interest rate, and time duration, with two main types: simple interest, calculated only on the principal amount, and compound interest, which accrues on both the principal and accumulated interest. Financial institutions use interest calculations to set loan terms, savings plan yields, and investment returns. Accurate interest computation is essential for consumer loans, mortgage amortization, bond valuation, and financial forecasting.
Source and External Links
Annual Percentage Rate (APR) vs. Effective Annual Rate (EAR) Formulas, Differences, and Applications - APR is the stated annual interest rate without compounding, while EAR reflects the actual annual interest considering compounding frequency, making EAR always equal to or higher than APR if compounding occurs more than once a year.
APR vs EAR | Definition, Key Differences, & Influencing Factors - APR is a simple annual interest rate used to compare loan costs, whereas EAR incorporates compounding within the year and thus shows the true cost or yield of a loan or investment.
Interest Rates 101: APR vs. EIR - The Effective Interest Rate (EIR), synonymous with EAR, accounts for compounding interest, making it a more comprehensive measure than APR, which excludes the effect of compounding and is therefore a nominal rate.
FAQs
What is the Effective Annual Rate?
The Effective Annual Rate (EAR) is the interest rate that reflects the total annual cost of borrowing or return on investment, accounting for compounding within the year.
What does Annual Percentage Rate mean?
Annual Percentage Rate (APR) represents the yearly cost of borrowing, including interest and fees, expressed as a percentage of the principal loan amount.
How do you calculate Effective Annual Rate?
Effective Annual Rate (EAR) = (1 + periodic interest rate) ^ number of periods per year - 1.
How is Annual Percentage Rate calculated?
Annual Percentage Rate (APR) is calculated by taking the total interest and fees paid over a year, dividing by the loan amount, and expressing the result as a yearly percentage rate.
What is the main difference between Effective Annual Rate and Annual Percentage Rate?
Effective Annual Rate (EAR) accounts for compounding interest within a year, showing the true annual return, while Annual Percentage Rate (APR) represents the yearly interest rate without compounding, often excluding fees.
Why does compounding frequency affect the Effective Annual Rate?
Compounding frequency affects the Effective Annual Rate because more frequent compounding periods increase interest-on-interest accumulation, resulting in a higher EAR compared to less frequent compounding.
When should you use Effective Annual Rate instead of Annual Percentage Rate?
Use Effective Annual Rate (EAR) instead of Annual Percentage Rate (APR) to accurately compare loans or investments with compounding interest periods within a year.
 calledges.com
calledges.com