Monte Carlo Simulation uses random sampling to model and analyze the behavior of complex systems under uncertainty, generating a wide range of possible outcomes based on probabilistic inputs. Historical Simulation relies on past market data to estimate risk and volatility, assuming that historical patterns can predict future movements. Explore the advantages and limitations of both methods to determine the best approach for your risk management strategy.
Main Difference
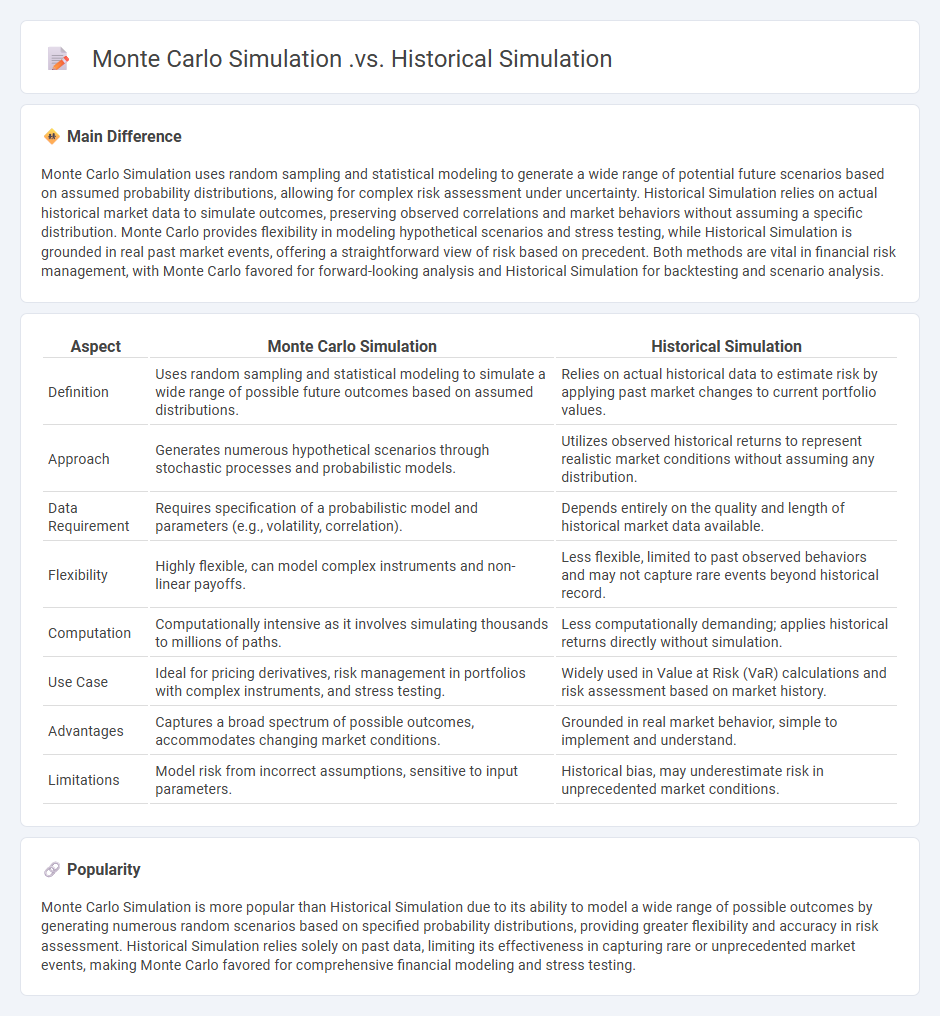
Monte Carlo Simulation uses random sampling and statistical modeling to generate a wide range of potential future scenarios based on assumed probability distributions, allowing for complex risk assessment under uncertainty. Historical Simulation relies on actual historical market data to simulate outcomes, preserving observed correlations and market behaviors without assuming a specific distribution. Monte Carlo provides flexibility in modeling hypothetical scenarios and stress testing, while Historical Simulation is grounded in real past market events, offering a straightforward view of risk based on precedent. Both methods are vital in financial risk management, with Monte Carlo favored for forward-looking analysis and Historical Simulation for backtesting and scenario analysis.
Connection
Monte Carlo Simulation and Historical Simulation are connected through their use in risk management and financial modeling to estimate potential future outcomes based on past data and probabilistic scenarios. Monte Carlo Simulation generates numerous random scenarios based on statistical distributions, while Historical Simulation relies directly on actual historical market data to assess risk and value at risk (VaR). Both methods complement each other by providing diverse approaches to quantify uncertainty and inform decision-making in finance.
Comparison Table
| Aspect | Monte Carlo Simulation | Historical Simulation |
|---|---|---|
| Definition | Uses random sampling and statistical modeling to simulate a wide range of possible future outcomes based on assumed distributions. | Relies on actual historical data to estimate risk by applying past market changes to current portfolio values. |
| Approach | Generates numerous hypothetical scenarios through stochastic processes and probabilistic models. | Utilizes observed historical returns to represent realistic market conditions without assuming any distribution. |
| Data Requirement | Requires specification of a probabilistic model and parameters (e.g., volatility, correlation). | Depends entirely on the quality and length of historical market data available. |
| Flexibility | Highly flexible, can model complex instruments and non-linear payoffs. | Less flexible, limited to past observed behaviors and may not capture rare events beyond historical record. |
| Computation | Computationally intensive as it involves simulating thousands to millions of paths. | Less computationally demanding; applies historical returns directly without simulation. |
| Use Case | Ideal for pricing derivatives, risk management in portfolios with complex instruments, and stress testing. | Widely used in Value at Risk (VaR) calculations and risk assessment based on market history. |
| Advantages | Captures a broad spectrum of possible outcomes, accommodates changing market conditions. | Grounded in real market behavior, simple to implement and understand. |
| Limitations | Model risk from incorrect assumptions, sensitive to input parameters. | Historical bias, may underestimate risk in unprecedented market conditions. |
Probability Distribution Assumptions
Probability distribution assumptions in finance often rely on the normal distribution to model asset returns, despite empirical evidence of fat tails and skewness. Financial models like the Black-Scholes option pricing model assume log-normal distribution of stock prices, which simplifies risk assessment and derivative pricing. However, real-world financial data frequently exhibit leptokurtosis and volatility clustering, leading to the adoption of alternative distributions such as the Student's t-distribution or stable Paretian distributions. Accurate probability distribution assumptions are critical for portfolio optimization, risk management, and stress testing in financial markets.
Scenario Generation
Scenario generation in finance involves creating multiple plausible future states of financial markets to assess risks and optimize portfolio management. Techniques such as Monte Carlo simulations, historical simulations, and stressed scenarios help model potential asset price movements, interest rate changes, and credit events. Financial institutions utilize scenario generation to comply with regulatory requirements like Basel III and to support stress testing under frameworks mandated by the Federal Reserve and European Central Bank. Accurate scenario generation enhances risk measurement models, improves capital allocation, and supports strategic decision-making under uncertainty.
Historical Data Dependency
Historical data dependency in finance refers to the reliance on past market information, such as stock prices, interest rates, and economic indicators, to inform investment strategies and risk assessments. Time series models like ARIMA and GARCH often use historical data to forecast future price movements and volatility. Portfolio managers analyze historical returns and correlations to optimize asset allocation and minimize risk exposure. Accurate interpretation of historical financial data supports decision-making processes, improving predictive accuracy and strategic planning.
Risk Measurement Accuracy
Risk measurement accuracy in finance critically influences portfolio optimization, regulatory compliance, and capital allocation. Advanced quantitative models, such as Value at Risk (VaR) and Conditional Value at Risk (CVaR), are employed to estimate potential losses under various market conditions with heightened precision. Incorporating real-time data analytics and machine learning algorithms enhances predictive capabilities, reducing model risk and improving decision-making reliability. Accurate risk assessment helps financial institutions maintain solvency and supports effective risk-adjusted performance evaluation.
Stress Testing Capabilities
Stress testing in finance evaluates the resilience of financial institutions under extreme but plausible adverse scenarios, such as market crashes, interest rate shocks, or liquidity shortages. Banks and regulators use stress tests to identify vulnerabilities in capital adequacy, risk management, and operational processes, ensuring compliance with Basel III and Dodd-Frank Act requirements. Advanced quantitative models simulate macroeconomic variables, credit defaults, and market volatility to forecast potential losses and liquidity gaps. Results guide strategic decisions, capital planning, and regulatory reporting to enhance systemic stability and protect stakeholders.
Source and External Links
Historical Simulation Vs Monte Carlo Simulation - Finance Train - This article compares historical simulation, which relies on past data, with Monte Carlo simulation, which uses random scenarios to estimate potential outcomes.
Monte Carlo Simulation vs. Historical Simulation - YouTube - This video discusses the differences between Monte Carlo simulations, which use statistical distributions, and historical simulations, which use past data to predict future outcomes.
Historical Simulation - What It Is, Examples, Vs Monte Carlo - This article explains how historical simulations use past data to model financial scenarios, while Monte Carlo simulations use random number generation to model risk factors.
FAQs
What is a Monte Carlo simulation?
Monte Carlo simulation is a statistical technique that uses random sampling and probabilistic modeling to estimate the outcomes of complex systems or processes.
What is a historical simulation?
A historical simulation is a method used in finance to assess risk by applying actual past market data and events to current portfolios to evaluate potential outcomes.
How do Monte Carlo and historical simulation methods differ?
Monte Carlo simulation uses random sampling and statistical modeling to estimate risk and financial outcomes, while historical simulation relies on actual historical market data to assess potential losses without assuming specific probability distributions.
What data is needed for a Monte Carlo simulation?
Monte Carlo simulation requires input variables with defined probability distributions, the mathematical model or system to analyze, and parameters for the number of simulation iterations.
What are the advantages of historical simulation?
Historical simulation advantages include simplicity in implementation, no need for distributional assumptions, direct use of actual historical data, and effective reflection of empirical correlations and market conditions.
When should Monte Carlo simulation be used?
Monte Carlo simulation should be used when modeling complex systems with inherent uncertainty, performing risk assessment, or evaluating probabilistic outcomes that cannot be solved analytically.
What are the limitations of historical simulation?
Historical simulation is limited by its reliance on past data, inability to capture unprecedented market events, assumption that historical patterns repeat, sensitivity to the chosen historical period, and potential to underestimate risk in volatile or evolving markets.
 calledges.com
calledges.com