Homoskedasticity refers to the condition in regression models where the variance of errors remains constant across all levels of an independent variable, ensuring reliable statistical inferences. Heteroskedasticity occurs when error variances fluctuate with the independent variable, potentially leading to inefficient estimates and biased standard errors. Explore detailed examples and detection methods to better understand these concepts.
Main Difference
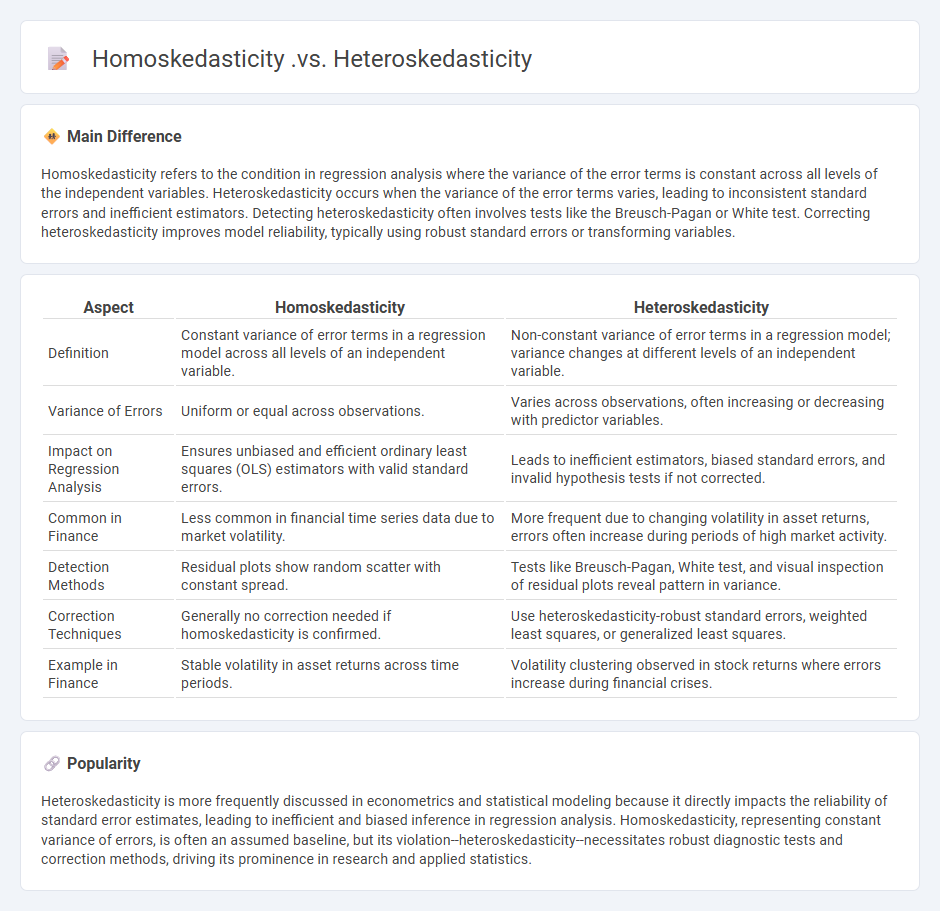
Homoskedasticity refers to the condition in regression analysis where the variance of the error terms is constant across all levels of the independent variables. Heteroskedasticity occurs when the variance of the error terms varies, leading to inconsistent standard errors and inefficient estimators. Detecting heteroskedasticity often involves tests like the Breusch-Pagan or White test. Correcting heteroskedasticity improves model reliability, typically using robust standard errors or transforming variables.
Connection
Homoskedasticity and heteroskedasticity refer to the variance of the error terms in a regression model, where homoskedasticity indicates constant variance across all levels of the independent variables, and heteroskedasticity indicates varying variance. Detecting heteroskedasticity is crucial because it violates the classical linear regression assumptions, leading to inefficient estimators and invalid standard errors. Techniques such as the Breusch-Pagan test or White test are commonly used to identify heteroskedasticity, helping to decide whether to apply robust standard errors or transform the model.
Comparison Table
| Aspect | Homoskedasticity | Heteroskedasticity |
|---|---|---|
| Definition | Constant variance of error terms in a regression model across all levels of an independent variable. | Non-constant variance of error terms in a regression model; variance changes at different levels of an independent variable. |
| Variance of Errors | Uniform or equal across observations. | Varies across observations, often increasing or decreasing with predictor variables. |
| Impact on Regression Analysis | Ensures unbiased and efficient ordinary least squares (OLS) estimators with valid standard errors. | Leads to inefficient estimators, biased standard errors, and invalid hypothesis tests if not corrected. |
| Common in Finance | Less common in financial time series data due to market volatility. | More frequent due to changing volatility in asset returns, errors often increase during periods of high market activity. |
| Detection Methods | Residual plots show random scatter with constant spread. | Tests like Breusch-Pagan, White test, and visual inspection of residual plots reveal pattern in variance. |
| Correction Techniques | Generally no correction needed if homoskedasticity is confirmed. | Use heteroskedasticity-robust standard errors, weighted least squares, or generalized least squares. |
| Example in Finance | Stable volatility in asset returns across time periods. | Volatility clustering observed in stock returns where errors increase during financial crises. |
Variance Consistency
Variance consistency in finance measures the stability of asset return volatility over time, crucial for accurate risk assessment and portfolio optimization. Stable variance allows models like GARCH (Generalized Autoregressive Conditional Heteroskedasticity) to predict future volatility more reliably, enhancing financial decision-making. Financial institutions rely on variance consistency to estimate Value at Risk (VaR) and to price derivatives effectively under varying market conditions. Empirical studies show that inconsistent variance can lead to underestimated risks and mispriced assets, impacting investment performance and regulatory compliance.
Error Term
The error term in finance represents the difference between the observed value and the value predicted by a financial model, capturing the impact of unobserved factors or random noise. It plays a critical role in regression analysis and risk modeling by accounting for deviations caused by market inefficiencies, measurement errors, or unexpected events. Quantifying the error term is essential for improving model accuracy and assessing the reliability of investment forecasts. Statistical techniques such as Ordinary Least Squares (OLS) help estimate the error term to refine predictive performance in asset pricing and portfolio management.
Regression Analysis
Regression analysis in finance quantifies relationships between variables, such as stock prices and economic indicators, to predict future trends. It is widely used for portfolio management, risk assessment, and forecasting asset returns by analyzing historical financial data. Linear regression models help determine the impact of interest rates, inflation, and GDP growth on securities performance. Advanced techniques like multiple regression and logistic regression enhance financial decision-making by identifying influential factors in market behavior.
Volatility Clustering
Volatility clustering refers to the empirical phenomenon in finance where large changes in asset prices are likely to be followed by large changes, and small changes tend to be followed by small changes, indicating persistence in volatility over time. This pattern is commonly observed in financial markets, such as equities, foreign exchange, and commodities, reflecting periods of high and low volatility clustering together. Models like GARCH (Generalized Autoregressive Conditional Heteroskedasticity) are widely used to capture and forecast volatility clustering effects in time series data. Understanding volatility clustering improves risk management, option pricing, and portfolio optimization by providing more accurate estimates of market behavior.
Statistical Inference
Statistical inference in finance involves using data-driven methods to estimate and test hypotheses about financial markets and instruments. Techniques such as regression analysis, hypothesis testing, and Bayesian inference help quantify risks, optimize portfolios, and forecast asset prices. Financial institutions rely on these methods to analyze historical returns, volatility, and correlations, enabling data-supported decision-making. Tools like Monte Carlo simulations and maximum likelihood estimation are integral for modeling complex financial phenomena and pricing derivatives.
Source and External Links
Heteroskedasticity - Definition, Causes, Vs Homoskedasticity - Homoskedasticity refers to equal variance of residuals across values of an independent variable, while heteroskedasticity means unequal variance of residuals, often seen as a problem in regression analysis, with heteroskedasticity being more common in real-world data.
Learn Homoscedasticity and Heteroscedasticity - Homoskedasticity means the error term has constant variance across different values of the independent variable, which is a key assumption in linear regression, whereas heteroskedasticity occurs when error variance changes, leading to potential inaccuracies in inference.
Homoscedasticity and heteroscedasticity - Statistically, homoscedasticity means the variance of the error term is constant (\(\sigma^2\)) for all observations, while heteroscedasticity arises when error variance depends on the observation or the independent variable, violating standard assumptions of regression models.
FAQs
What is homoskedasticity in statistics?
Homoskedasticity in statistics refers to the condition where the variance of the error terms or residuals in a regression model remains constant across all levels of the independent variable(s).
What is heteroskedasticity and how does it differ from homoskedasticity?
Heteroskedasticity occurs when the variance of the error terms in a regression model is not constant across observations, causing inconsistent standard errors and inefficient estimates. Homoskedasticity means the error terms have constant variance, ensuring reliable hypothesis testing and efficient estimators.
Why is homoskedasticity important in regression analysis?
Homoskedasticity is important in regression analysis because it ensures constant variance of the error terms, which validates the efficiency of ordinary least squares (OLS) estimators and the accuracy of standard errors, confidence intervals, and hypothesis tests.
How can you detect heteroskedasticity in a dataset?
Detect heteroskedasticity by visualizing residuals versus fitted values for patterns, conducting the Breusch-Pagan test, White test, or Goldfeld-Quandt test, and analyzing variance changes in residuals across different levels of an independent variable.
What are the causes of heteroskedasticity?
Heteroskedasticity is caused by factors such as model misspecification, omitted variables, measurement errors, non-constant variance in error terms due to changes in scale or heterogeneity in the data, and structural changes or outliers.
How do you fix or handle heteroskedasticity in a model?
Fix heteroskedasticity by applying robust standard errors, transforming variables (e.g., log transformation), using weighted least squares (WLS), or specifying a heteroskedasticity-consistent covariance matrix estimator.
What are the consequences of ignoring heteroskedasticity?
Ignoring heteroskedasticity leads to inefficient and biased standard error estimates, resulting in invalid hypothesis tests and confidence intervals in regression analysis.
 calledges.com
calledges.com